
Pelaa Futoshiki Puzzlesia verkossa
Seuraavassa tutoriaalissa esitellään askel askeleelta Futoshiki-pulmien perus- ja edistyneitä ratkaisutekniikoita, ja mukana on kuvia, jotka havainnollistavat menetelmiä tietyillä lautakokoonpanoilla.
Ratkaisun löytämisen lähtökohtana on itse pelin määritelmä: Futoshiki vaatii käyttäjää löytämään pelilaudan, jossa jokainen numero esiintyy kerran jokaisella rivillä ja sarakkeessa noudattaen pelilaudan epäyhtälöitä. Tämän kriteerin avulla ratkaisuun voidaan edetä täyttämällä askel askeleelta tyhjiä pelilaudan ruutuja tietyillä numeroilla, koska ne ovat ainoa tapa noudattaa pelilaudan rajoituksia.
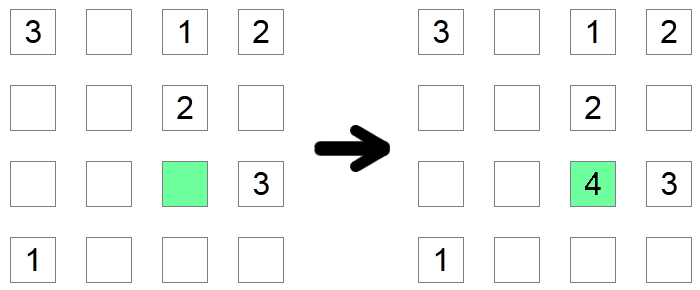
Jos ruudun sarake ja rivi sisältävät jo kaikki mahdolliset numerot yhtä lukuun ottamatta, niin kyseisen ruudun on sisällettävä puuttuva numero. Yllä olevassa esimerkissä vihreän ruudun on oltava 4, koska sillä ei voisi olla mitään muuta arvoa, koska muut mahdolliset numerot löytyvät jo sen riviltä tai sarakkeesta.
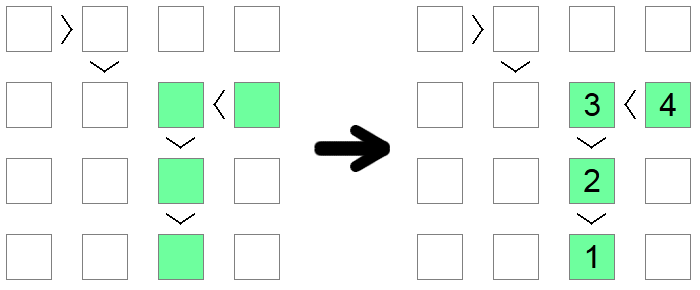
Jos huomaat epäyhtälöketjun, olipa se joko < (kaikki nouseva) tai > (kaikki laskeva), joka on kooltaan yhtä suuri kuin pelilaudan koko, ketjun täytyy olla jono luvusta 1 ylöspäin pelilaudan pituuteen. Ketjun pituus takaa, että tämä jono on ainoa mahdollinen ratkaisu, joka täyttää epäyhtälöketjun asettaman monotonisen ehdon.
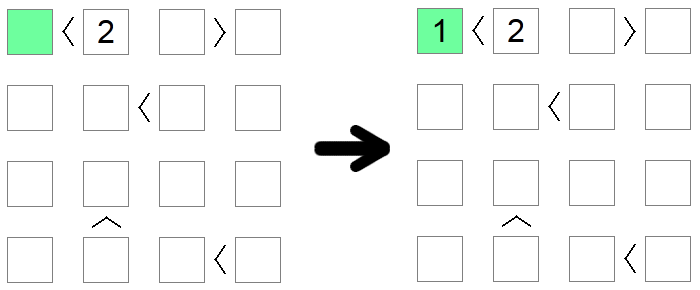
Neliöiden, joiden arvo on alle 2, arvo on implisiittisesti 1, koska se on ainoa sallittu arvo pelilaudalla, joka noudattaa tätä ehtoa. Vastaavasti neliöiden, jotka ovat suurempia kuin pelilaudan koko miinus 1, arvo on oltava yhtä suuri kuin pelilaudan koko. Yllä olevassa esimerkissä vihreän neliön (alle 2) ainoa mahdollinen arvo on 1.
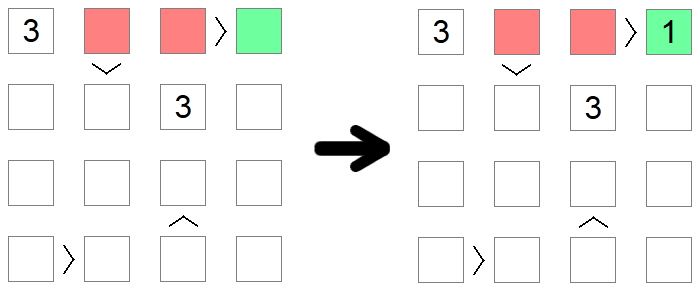
Neliöt, jotka ovat suurempia kuin muut neliöt, eivät voi olla arvoltaan 1 , joka on pelilaudan pienin sallittu arvo, koska ei ole arvoa, joka on pienempi kuin 1 Vastaavasti neliöt, jotka ovat pienempiä kuin muut neliöt, eivät voi sisältää suurinta sallittua arvoa, koska epäyhtälön toisella puolella ei olisi mitään suurempaa täytettävää. Yllä olevassa esimerkissä punaisia neliöitä ei voida täyttää arvolla 1 , koska ne kaikki ovat suurempia kuin muut pelilaudan neliöt, joten ainoa mahdollinen sijoitus numerolle 1 pelilaudan ensimmäisellä rivillä on vihreä ruutu.
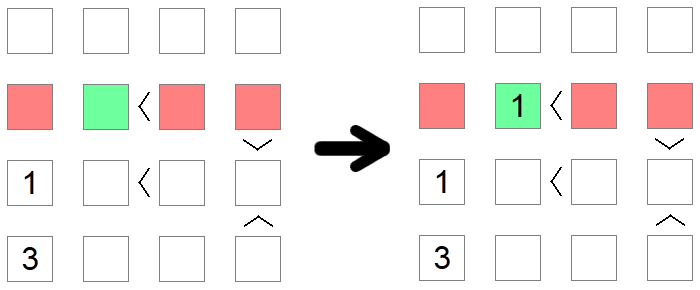
Joskus johtopäätökseen pääsemiseksi on käytettävä useita sääntöjä. Näin on yllä olevassa esimerkissä, jossa yritämme sijoittaa arvon 1 pelilaudan toiselle riville. Ensimmäinen punainen ruutu eliminoidaan sarakkeen poissulkemisen vuoksi (meillä on jo 1 kyseisessä sarakkeessa), kun taas toinen ja kolmas punainen ruutu eliminoidaan minimiarvojen poissulkemisen vuoksi, koska näihin kohtiin liittyy 'suurempi kuin' -epäyhtälöitä. Siksi vihreä ruutu on ainoa mahdollinen paikka luvun 1 sijoittamiseksi kyseiselle riville.
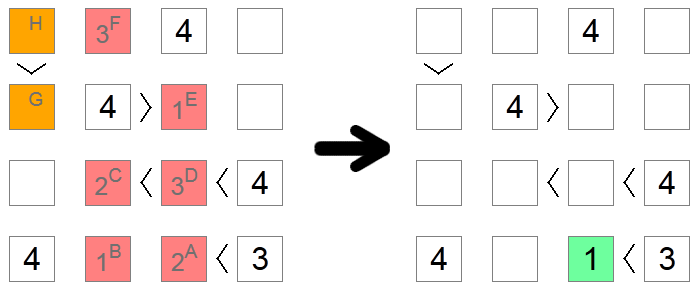
Joskus, etenkin vaikeilla pelilaudoilla, ei ole muita tapoja selvittää neliön oikeaa numeroa kuin sukeltaa kunkin mahdollisuuden seurauksiin, kunnes löydetään ristiriita. Yllä olevassa esimerkissä kaikki punaiset ja oranssit neliöt ovat aluksi tyhjiä. Haluamme selvittää, sisältääkö ruutu A luvun 1 vai 2 Oletamme, että se sisältää luvun 2, ja tarkistamme, löydämmekö ristiriidan tämän oletuksen perusteella.
Jos ruudun A arvo on 2, niin ruudun B arvo olisi 1 (ainoa jäljellä oleva arvo alimmalla rivillä). Ruutu C voi olla 1 tai 2, koska siinä on epäyhtälöiden ketju, joka vaatii kaksi suurempaa lukua, mutta nyt se ei voi olla 1 ruudun B sarakepoikkeamisen vuoksi, joten ruutu C on 2 ja ruutu D on 3 (ainoa arvo 2:n ja 4:n välillä). Sarakepoikkeamien vuoksi ruutu E on 1 ja ruutu F on 3.
Jos nyt tarkastelemme oransseja neliöitä, huomaamme ristiriidan: jos ruutu G olisi 2, ruudun H pitäisi olla joko 3 tai 4 , mikä ei ole sallittua rivien poissulkemisen vuoksi. Jos ruutu G olisi 3, ruudun H pitäisi olla 4, mikä ei ole sallittua samasta syystä. Koska meillä ei enää ole jäljellä olevia arvoja ruudulle G, se tarkoittaa, että olemme päätyneet umpikujaan ja alkuperäinen oletuksemme oli väärä: 2 ei ole kelvollinen siirto ruudulle A, joten voimme mennä eteenpäin ja sijoittaa siihen 1, joka on ainoa muu mahdollinen arvo.
Olemme yllä osoittaneet, kuinka ratkaista futoshiki-pulma onnistuneesti käsittelemällä erilaisia tekniikoita, jotka auttavat sinua päättelemään seuraavan siirron jopa vaikeissa tilanteissa. Toinen tärkeä tekijä futoshiki-pulmien ratkaisemisen taitavuudessa ja nopeudessa on kokemus: mitä enemmän harjoittelet, sitä paremmaksi ja nopeammaksi tulet.
Jos olet valmis haasteeseen, voit pelata heti satunnaista Futoshiki-pulmaa napsauttamalla alla olevaa painiketta. Onnea!
© 2026 - Kaikki oikeudet pidätetään - Noin - Tietosuojakäytäntö - DA | DE | EN | ES | ET | FI | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR